
“If the Left were to abstain from participating in this election en masse, the consequences would be deep.”
The end of Senator Bernie Sanders’ campaign is a clear setback to the American Left in the electoral arena. Importantly, this is the second time this has happened. The end of the 2016 Democratic primary, even though it ended with a similar defeat for the Left, was a victory in important ways. The 2020 primary largely revolved around the issues set by the Sanders campaign in 2016, and Senator Sanders went from being a virtually unknown politician to a national phenomenon. This time, however, the stage was set for Senator Sanders to win the Democratic nomination. The campaign already had a nationwide operation set up before any of his rivals, and the conversation inside the Democratic Party had been essentially built by the Left. What is more, the race was looking up for Senator Sanders until Super Tuesday when a series of perfectly timed campaign suspensions and endorsements overturned the results expected from the polls. Importantly, there is some evidence that the party machinery actively engaged in the process behind the scenes. In the end, the establishment of the party won again, and now even Senator Sanders has endorsed former Vice President Biden. All of these issues put the American Left in a very difficult position. Senator Sanders’ endorsement means little to nothing. Left-wing organizations already issued a large list of demands that would have to be met before they would consider endorsing Vice President Biden. These are demands that, in my opinion, are very unlikely to be met. So with a grim outlook for personnel or policy concessions from the Biden campaign, all that the Left has on its arsenal is organizing around a voting strategy, for which there are few options. Yet none are optimal.
To understand what is the best course of action, it is important to look—not just at the immediate choice before the Left—but at the long term, through the lenses of history and party demographics. One model that I believe is highly relevant for the present political moment, especially from the perspective of the Left, is that of critical realignment and realigning elections. This was originally developed by Harvard political scientist V. O. Key and then further expanded by his mentee, Walter Dean Burnham. Critical realignment is a historical model devised to explain how particular elections—provided the correct demographic composition—can have a decisive impact on political party dynamics. Like any model, it has limitations and is not meant to explain everything. Instead, it tries to capture important aspects about historical events. There is much debate about whether the critical realignment model continues to be relevant—or if it is only useful to explain the past. In fact, one of the more recent scholarly works on the subject is a book edited in 1991 by Byron E. Shafer titled The End of Realignment?: Interpreting American Electoral Eras. It includes a chapter by Burnham entitled “Critical Realignment: Dead or Alive?,” in which the author gives two conditions that must be met for an election to be critical. First, politically relevant minorities must change their voting patterns, whether that means switching parties, start voting when they previously did not, or vice versa. Secondly, this shift must have significant and enduring consequences in the political landscape. These can come in the form of changing policy priorities, a change in the dominant political parties or elites, or an alteration in the constitutional roles of different branches of government, among others. Two clear and generally accepted examples, therefore, include the 1860 election (in which the Republican Party supplanted the Whig Party as one of the two dominant party forces) and the 1932 election (which ushered in the New Deal coalition).
Realignment is not usually seen as a deliberate strategy of change. That is, voters in the 1860 presidential election were not looking for long-term change to the party structure of the United States. It is, of course, possible that some people did, but it was not a concerted effort as much as a confluence of many factors. That does not mean it cannot be used as such. This is especially true given that all the necessary conditions are set for a realigning election, and it looks as though the coalition of Left-wing voters and organizations could be one of the politically relevant minorities present in realigning elections. To see why, we need to understand the current configuration of the American Electorate. Political scientist Lee Drutman has done an in-depth analysis of the voting patterns of Americans in the 2016 election, according to their ideology. One of his most striking findings becomes readily visible when looking at a graphic that maps Americans’ ideology along two different axes, along with their presidential candidate of choice. The resulting graphic looks like this:
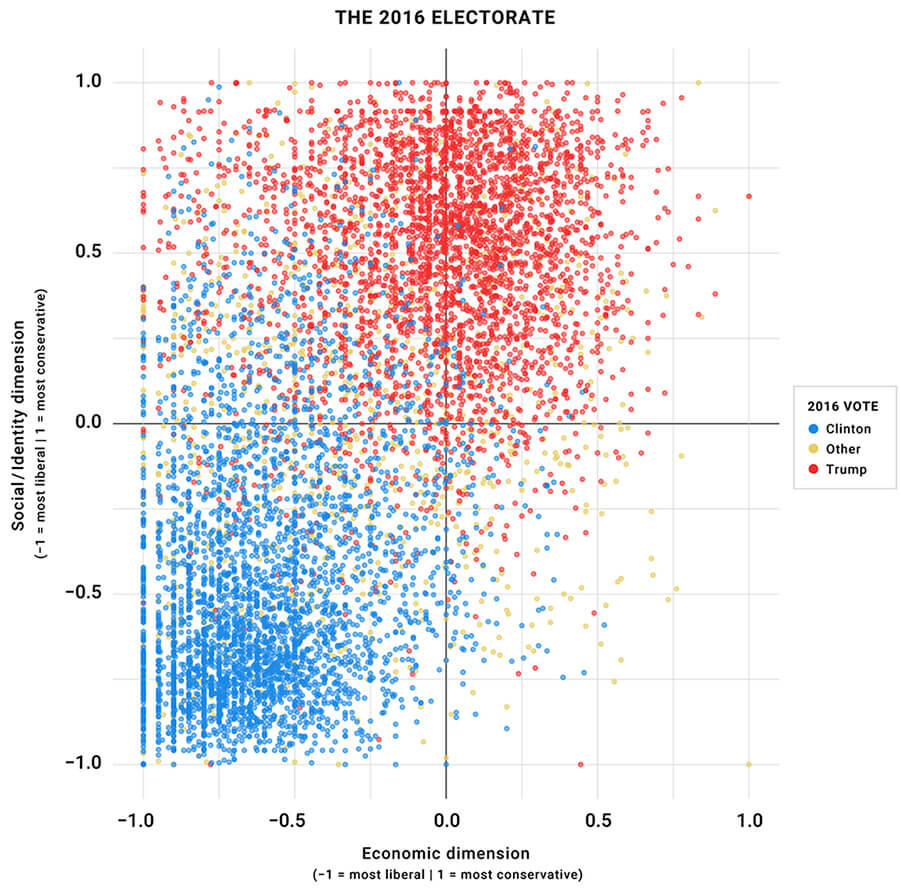
The horizontal axis measures voters’ position on economic issues, while the vertical axis maps their stances on social and cultural issues. Drutman divides the electorate according to the four resulting quadrants. Starting from the top left and moving clockwise he calls them populists, conservatives, libertarians and liberals. The largest of the four is the liberals, which make up 44.6% of the electorate. This is followed by populists with 28.9%, then conservatives at 22.7%. Libertarians are far and away the smallest group, comprising not even 4% of American voters.
Yet, these findings show that the prevailing elite narrative, one that largely drove the short lived candidacies of Michael Bloomberg and Howard Schultz, is a complete fabrication.
This has several important implications. Under the understanding that the Democratic Party is economically and socially liberal—and the Republicans are fiscally and socially conservative—there are two underrepresented ideological groups: libertarians and populists. Yet, these findings show that the prevailing elite narrative, one that largely drove the short lived candidacies of Michael Bloomberg and Howard Schultz, is a complete fabrication. These two candidates’ theory of the electorate was that swing voters are the suburban socially liberal but fiscally conservative voters. Now, while it is true that this group is largely swing voters (they were almost evenly split between then-candidate Donald Trump, former Secretary of State Hillary Clinton, and third parties), it is a group so insignificant in terms of voting power that it should barely merit the attention of anyone thinking about electoral strategy. The more pressing issue is that this now seems to be much of the basic thinking behind Vice President Biden’s campaign. Vice President Biden has backed cuts to the social safety net, and, as the presumptive democratic nominee, he continues to oppose universal programs, such as single-payer healthcare. He even went as far as to say that, as president, he would veto a single-payer bill that had managed to clear every obstacle in congress. Others in the Democratic Party elite have similarly expressed contempt for economically left-wing policies such as Medicare For All and the Green New Deal. In short, Democratic elites continue to push the party ever more into the “libertarian” quadrant, conceding to the left-wing of the party on social issues but rarely giving ground on the economy.
It should be obvious why this is a problem for the Democratic Party’s long term electoral success. Not only is the party moving ever closer to the smallest ideological demographic, but it is also moving away from the largest cluster of swing voters as things presently stand, namely, populists. To put it differently, in economic terms, the American electorate is largely on the Left, with populists and liberals combined making up 73.5% of it. On cultural and social issues, the field is much more divided, but conservatives still narrowly edge out liberals with populists and conservatives adding up to 51.6%. One caveat is that the placement of the axes is arbitrary, and perhaps in Drutmans study, one might argue, they are placed too far to the right. This would mean, among other things, that the economic left is artificially large and that the mythical suburban voters are classified in this case as economically center-left, rather than center-right. There is some evidence that this might be at play. For example, looking at the graphic, there is a large group of voters that are placed on the left end of the chart, while there is virtually no one on the right end. This is not how data normally behaves. A plot with a more natural spread out distribution would have its center further to the left, which would decrease the percentage of those classified as populists and liberals and increase conservatives and libertarians. Another piece of evidence is that suburban voters were an important factor in giving the Democrats their 2018 victory in the House, meaning they probably are not such a small constituency.
All that being said, it still seems likely that the economic left is an overall majority and even more so within the Democratic Party. Senator Sanders’ Medicare For All proposal is backed by a majority of all voters. Among Democrats, it is overwhelmingly favored with 77% approval. Elites in Washington are correct about one thing: cultural issues are the most salient dividing line in American politics. Where they could not be more mistaken is in their idea that the country is on the center-right economically. One fact that cannot be stressed enough is that what ultimately won Vice President Biden the nomination was the perception that he is better positioned than Senator Sanders to beat President Trump. But exit polls—state after state—have shown that Senator Sanders’ policy agenda is more popular, even in states where Vice President Biden won overwhelmingly like South Carolina.
But this and the last election cycles should have made it clear that the Democratic Party is just as hostile to left-wing values, even if less openly.
This means that the Left is in a position of power. The Democrats cannot win in November without the left-wing voters. If all of the previously presented data show anything, it has to be that. This shows why the Left is potentially the politically relevant minority in a future realigning election, which could be the next one. For decades, leftists have voted for the Democratic Party, even when it clearly does not represent its principles. It is simple to see why: the Republican Party, not only does not represent them, it is openly hostile to them. But this and the last election cycles should have made it clear that the Democratic Party is just as hostile to left-wing values, even if less openly. In many ways, the Democrats are much more of a barrier to structural change in a left-wing direction than the Republican party. The latter, of course is clearly much further to the right. However, the former functions as a gatekeeper of what constitutes an acceptable alternative. In this case, the alternative seems to be increasingly moving towards the economic right.
If the Left were to abstain from participating in this election en masse, the consequences would be extensive. First, it would certainly be a case of a politically relevant minority changing its voting patterns, as critical realignment theory indicates. The Republicans would likely win a landslide victory, possibly in all branches, of course. But perhaps more importantly, it would be the kind of failure that the leadership of the Democratic Party could not simply argue away. In 2016, it was possible to point to the electoral college system, or to the Green Party, or to Russia. But there is no amount of hand waving that can excuse responsibility for a landslide loss. It would signal that the Left is the constituency that the Democratic party needs to serve. And finally, in line with critical realignment theory, an election with results with such an impact are exactly the kind that push the political system towards realignment.
Of course, there are multiple ramifications that need to be factored in, though perhaps the single most important one is the Supreme Court. There is a good chance that a new Justice will be selected within the next four years; and, under a Republican administration, it would mean that the Court would lean even more to the Right than it does now. However, even if there is no coordinated effort from the Left to stay out, it is likely that President Trump will win again anyway. Vice President Biden might be up in the polls at the moment, but so was Secretary Clinton on election night. And besides, in the end, national polls are irrelevant. Vice President Biden has much of the same baggage that cost Secretary Clinton losses in the key states of Michigan, Wisconsin, and Pennsylvania—not to mention sexual assault accusations, which come in the wake of the #MeToo movement. And lastly, it is difficult to say what Senator Sanders’ supporters will do come November. The political climate and anecdotal evidence would suggest that they are less likely to default to the Democratic nominee than in 2016, as a recent New York Times series of interviews with Senator Sanders’ supporters found.
Now, there is no guarantee that President Trump will surely win. I think it is likely, but we are in an unprecedented situation. A global pandemic is still happening, and it may have deep economic consequences, so any prediction for November should be treated with caution. Now, if a victory by President Trump were assured, the following assertion should be uncontroversial from the point of view of the Left: a landslide Republican victory is preferable to a slim one. It may sound controversial, but I do not believe it is. One argument against it might be that a landslide win gives the Republicans a much stronger mandate. The problem with this argument is that, unlike the Democrats, Republicans understand power and use it, as shown, for example, during the Merrick Garland confirmation hearings that never took place. So no matter how much of a mandate they have, they will try to pass the same policy and legislation. The policy consequences of a slim and a landslide Republican victory will be the same. The difference is that a slim Republican victory will result in no accountability for the Democrats, and a landslide will force it. The first case still leaves the Democratic Party as a viable alternative. The latter case poses serious questions. The problem, of course, is that a Republican victory is not a guarantee, so this is not very useful, except as a means to think about the implications of different defeat margins.
A slim Republican victory and a Democratic win, however, do have one thing in common: both are bound to maintain the current power and elite structure. The one issue where there is a substantive difference is the Supreme Court—and the impact it could have on abortion or LGBTQ rights. Now, this is by no means a small issue, and voting on it alone is a perfectly valid position. But even in the event of a victory for President Trump, not necessarily everything would be lost in this regard. Even moderate Democrats have been entertaining the idea of reforming the Supreme Court in a way that would allow for changes to the political composition overnight. Importantly, one of the cited reasons for it is the perception that Republicans’ tactics regarding this institution have completely thrown out the notion that it is an apolitical institution that should not be tampered with.
In the end, the Left desperately needs an outcome that takes power away from the Democratic leadership—or the Left will remain politically crippled for the foreseeable future. A mass abstention, I believe, has the best chance of producing that outcome.
This leaves us with the question of what would come next if a realignment indeed took place. Many have advocated for a multi-party democracy. Lee Drutman, the author of the previously cited study, is one of such people. The argument for it has several layers, including putting an end to congressional gridlock, fairness regarding the value of each vote, and others. But the most basic way of describing it is that, as his study shows, the American electorate is not composed of just two ideological groups. As such, the political system should reflect that. I do think this is a fair assessment, and I also think that more parties would be better in the long run. The one problem I see with this line of reasoning is that, as Drutman himself argues, this would require changing the electoral system. Majority voting, which is used in the United States, tends towards bipartisanship. Multiparty systems generally stem from proportional representation. This is known as Duverger’s Law, for French sociologist Maurice Duverger, who first observed and explained it. It is true that some places such as the United Kingdom have several parties and a majority system. But as political scientist Gary Cox has observed, if one looks at the constituency level party system, each individual constituency is essentially its own two-party system. In general, the number of parties is approximately one more than the total seats available by election. In the United Kingdom, regional politics means that the two dominant parties in each constituency are not always the same. But in the United States, where national politics seem to dominate the conversation, it will be difficult to maintain more than two parties without changing the electoral system.
I agree this should be pursued. However, I believe it is unlikely to happen—because the two parties have an interest in keeping the electoral system unchanged. In fact, I think Drutman’s vision is more likely to be realized in a situation in which one of the parties collapses under its own weight, which is what a mass abstention could accomplish.
In the end, I think that some form of realignment is bound to happen due to ideological demographics at some point in the near future. It could be this election, if the Left were to take the kind of action I am describing. In the media, it is already visible in some ways. A strong example is The Hill’s morning YouTube show Rising. The left-wing host, Krystal Ball, is very much in line with the Left as a movement, rather than the Democratic leadership and has been praised by the likes of Jacobin. The conservative host, Saagar Enjeti, used to be the White House correspondent for The Daily Caller, and is on the Right on many cultural issues, such as drugs. Yet, if one listens to the two discussing most of the issues that come up on the show, there seems to be more agreement than anything. This is mostly because they agree on a lot of economic issues, particularly regarding workers’ rights. Their jointly authored book, The Populist’s Guide to 2020, was a massive success in terms of sales, which indicates that their message has broad appeal.
With all of this in mind and with Drutman’s empirical findings, I see two possible new cleavages forming after a realignment, short of the move towards a multiparty system.
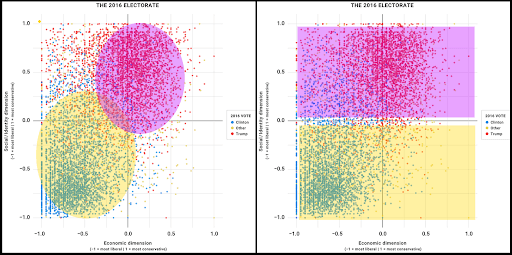
The first one, which is probably the more obvious, is something closer to what exists in European democracies. One party exists both in the economic and cultural left, and one in the economic and cultural right, but there is a center that is much closer to the economic left than what exists in the current American party system. Now, it might seem like that is what already exists, but it should be stressed that the graphic plots individual voters’ positions—not those of the parties. And, as was discussed, the base of the Democratic Party is considerably to the left of the party itself in economic terms. The other is one that is predicated purely on cultural issues. After all, on that axis, the American electorate is divided almost in half, according to Drutman’s findings. However, cultural and social issues evolve much more rapidly than economic ones, so in the end, I believe the first one is more likely to be stable. What should be absolutely clear, however, is that the current system is neither sustainable, nor desirable. And, whether it happens now or in a future election, it needs to be replaced.
Néstor de Buen holds an M.A. in social sciences from The University of Chicago. He has previously written at Quillette.










